Diverse
Oppgave
En bil kjører over en bakketopp som danner en del av en sirkel med en radius på \(r = 100 m\) (se bilde under). Det går da an å vise at dersom bilen kjører med konstant fart, vil den ha en akselerasjon på toppen av bakken gitt ved \(a = v^2/r\), hvor \(v\) er farten til bilen. Denne akselerasjonen virker inn mot sentrum av sirkelen.
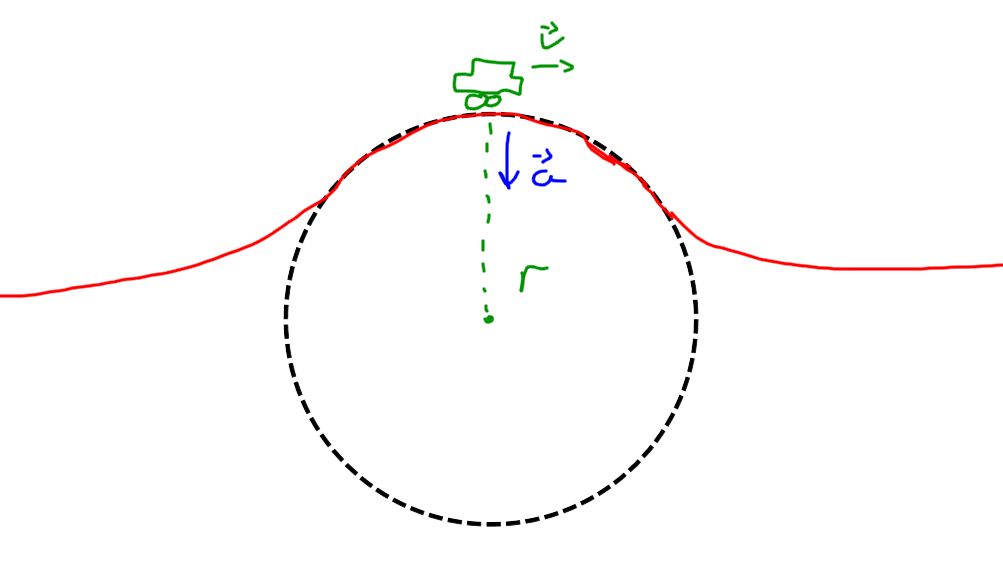
- Tegn på kreftene som virker på bilen i vertikal retning når den er på toppen av bakken.
- Hvis bilen kjører fort nok, vil den kunne lette fra bakken idet den kjører over toppen. Hvor fort må den kjøre for at dette skal skje? Gi svaret i km/h.
- I eksemplet antar vi at bilen har konstant fart over bakketoppen. Likevel har bilen en akselerasjon. Hvordan kan man ha en akselerasjon og samtidig konstant fart når akselerasjon er definert som endring i hastighet per tid?
Løsningsforslag
Oppg. a)
Det virker to krefter i vertikal retning på bilen når den er på bakketoppen. En kraft fra bakken som peker rett opp, og tyngdekraften som virker rett ned. Siden akselerasjonen til bilen er inn mot sentrum av sirkelen, dvs. rett ned, må tyngdekraften være større enn kraften fra bakken.
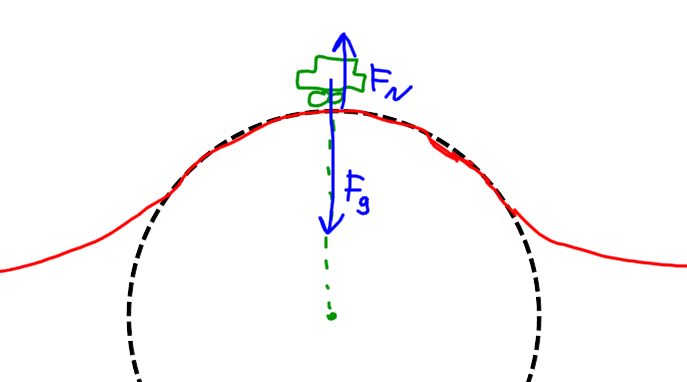
Oppg. b)
Dersom bilen mister kontakt med bakken, vil normalkraften være lik null. Det virker da kun tyngdekraft på bilen. Vi bruker Newtons andre lov og får:
\begin{align*} \sum F = ma &= F_g \\ m \frac{v^2}{r} &= mg \\ v^2 &= gr \\ v &= \sqrt{gr} \\ v &= \sqrt{9.8 \mbox{ m/s}^2 \cdot 100 \mbox{ m}} \\ v &= 31.3 \mbox{ m/s} \approx \underline{\underline{113 \mbox{ km/h}}} \end{align*}Oppg. c)
Fart og hastighet er ikke det samme. Bilen har konstant fart, men ikke konstant hastighet. Fart er tilbakelagt strekning per tidsenhet, dvs. i praksis hva speedometeret viser. Hastighet er endring i posisjon per tidsenhet. Hastighet har også en retning i tillegg til verdi. Siden bilen kjører over en sirkulær bakketopp, blir den romlige retningen bilen kjører hele tiden endret. Vi har dermed endring i hastighet, og dermed akselerasjon.