Krefter
Oppgave
En kloss A på 10 kg henger i en snor i taket. Under denne klossen er det festet en ny snor hvor det henger en kloss B på 5 kg i andre enden. En tredje kloss C på 2.5 kg er festet i en snor som henger under kloss B.
- Regn ut alle kreftene som virker på de ulike klossene.
- Anta at vi kutter snora mellom kloss A og kloss B. Finn nå verdien av de samme kreftene du regnet ut i oppgave a).
Løsningsforslag
Vi starter med å tegne en figur som viser alle kreftene på de ulike steinene hver for seg, i tillegg til å gi dem et navn slik at vi kjenner dem igjen i utregningene.
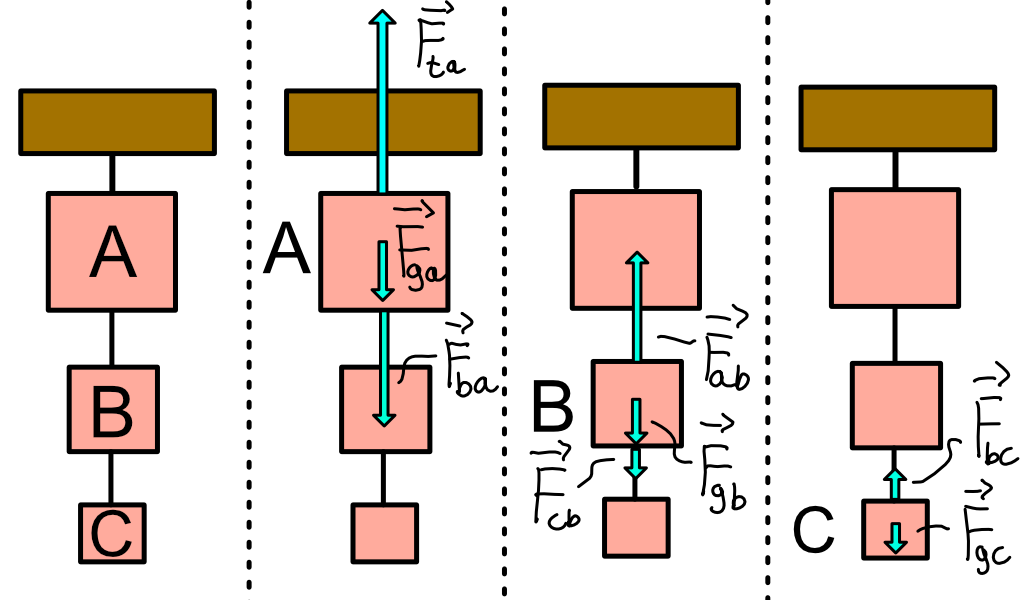
På stein C har vi to krefter, tyngdekraften \(F_{gc}\) og et snordrag fra kloss B \(F_{bc}\). Tyngdekraften finner vi ved å brukte uttrykket:
\begin{align*} F_{gc} = m_c g = 2.5\mbox{ kg} \cdot 9.8 \mbox{ m/s}^2 = 24.5 \mbox{ N} \approx 25 \mbox{ N} \end{align*}Siden steinen henger i ro, må summen av kreftene være lik null. Dette betyr at snordraget fra kloss B må være like stort som tyngdekraften, siden det er kun disse to kreftene som virker på kloss C, dvs.
\begin{align*} F_{bc} = 24.5 \mbox{ N} \approx 25 \mbox{ N} \end{align*}Kloss B blir påvirket av tre krefter; tyngdekraften \(f_{gb}\), en drakraft fra kloss C \(F_{cb}\) og et snordrag fra kloss A \(F_{ab}\). Drakraften fra kloss C er motkraften til kraften \(F_{bc}\) i henhold til Newtons tredje lov. Dette gir oss:
\begin{align*} F_{cb} = 24.5 \mbox{ N} \approx 25 \mbox{ N} \end{align*}Tyngdekraften får vi fra det vanlige uttrykket:
\begin{align*} F_{gb} = m_b g = 5 \mbox{ kg} \cdot 9.8 \mbox{ m/s}^2 = 49 \mbox{ N} \end{align*}Den siste kraften får vi fra Newtons første lov. Kloss B henger i ro, så summen av kreftene må være lik null. Dette gir oss:
\begin{align*} F_{ab} - F_{cb} - F_{gb} &= 0 \\ F_{ab} &= F_{gb} + F_{cb} \\ F_{ab} &= 49 \mbox{ N} + 24.5 \mbox{ N} \\ F_{ab} &= 73.5 \mbox{ N} \approx 74 \mbox{ N} \end{align*}Kloss A blir også påvirket av tre krefter; tyngdekraften \(F_{ga}\), en drakraft fra kloss B \(F_{ba}\) og et snordrag fra taket \(F_{ta}\). Drakraften \(F_{ba}\) er motkraften til \(F_{ab}\) i henhold til Newtons tredje lov. Dette gir oss:
\begin{align*} F_{ba} &= 73.5 \mbox{ N} \approx 74 \mbox{ N} \end{align*}Tyngdekraften får vi igjen fra det kjente uttrykket:
\begin{align*} F_{ga} = m_a g = 10 \mbox{ kg} \cdot 9.8 \mbox{ m/s}^2 = 98 \mbox{ N} \end{align*}Den siste kraften får vi igjen fra Newtons første lov:
\begin{align*} F_{ta} - F_{ba} - F_{ga} &= 0 \\ F_{ta} &= F_{ga} + F_{ba} \\ F_{ta} &= 98 \mbox{ N} + 73.5 \mbox{ N} \\ F_{ta} &= 171.5 \mbox{ N} \end{align*}