Elektrisitet
Oppgave
Du har to kretser, en med lyspærer koblet i serie (figuren til venstre) og en med lyspærer koblet i parallell (figuren til høyre). Når du kobler på en ekstra lampe i seriekoblingen, lyser alle lyspærene svakere. Når du kobler på en ekstra lampe i parallell på kretsen til høyre, ser du derimot at lyspærene lyser like sterkt som før. Anta at begge kretser er kobla til et 9.0 V batteri og at lyspærene er identiske med en resistans på 1.5 Ω, og at lyspærene følger Ohms lov.
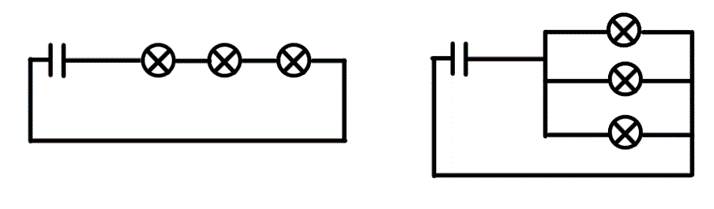
- Vis ved regning at strømmen gjennom lyspærene i seriekoblingen blir lavere når vi kobler på en ekstra lyspære i serie.
- Vis ved regning at strømmen gjennom lyspærene i parallellkoblingen forblir den samme selv etter at vi har koblet til en ekstra lyspære i parallell.
Løsningsforslag
a)La oss første regne strømmen som går gjennom lampene i seriekoblingen. Siden alle lampene er koblet i serie, vil den totale motstanden i kretsen være:
\begin{align*} R = 1.5 \ \Omega + 1.5 \ \Omega + 1.5 \ \Omega = 4.5 \ \Omega \end{align*}Vi finner da strømmen i kretsen ved å bruke Ohms lov:
\begin{align*} U &= RI \\ I &= \frac{U}{R} \\ I &= \frac{9 \mbox{ V}}{4.5 \ \Omega} \\ I &= 2 \mbox{ A} \end{align*}Dersom vi kobler til en ekstra lampe i serie, vil den totale motstanden i kretsen nå være:
\begin{align*} R = 1.5 \ \Omega + 1.5 \ \Omega + 1.5 \ \Omega + 1.5 \ \Omega = 6 \ \Omega \end{align*}Strømmen i kretsen blir nå:
\begin{align*} I &= \frac{U}{R} \\ I &= \frac{9 \mbox{ V}}{6 \ \Omega} \\ I &= 1.5 \mbox{ A} \end{align*}Strømmen gjennom pærene er lavere og pærene lyser svakere.
b)Siden hele kretsen består av èn enkelt parallellkobling, vil spenningsfallet over hver av grenene være like stort som spenningen til batteriet, dvs. 9 V. Strømmen gjennom en lampe blir da:
\begin{align*} I &= \frac{U}{R} \\ I &= \frac{9 \mbox{ V}}{1.5 \ \Omega} \\ I &= 6 \mbox{ A} \end{align*}Dette hadde vi strengt tatt ikke trengt å regne ut siden spenningen over hver av grenene blir det samme uansett hvor mange grener vi har. Så selv om vi legger til en ekstra lampe, vil vi fortsatt ha et spenningsfall på 9 V over denne lampen og strømmen blir fortsatt 6 A.
Vi kunne også vist det mer direkte. La oss regne ut den totale strømmen i kretsen. Siden alle tre lampene er koblet i parallell, vil den totale motstanden bli:
\begin{align*} \frac{1}{R} &= \frac{1}{1.5 \ \Omega} + \frac{1}{1.5 \ \Omega} + \frac{1}{1.5 \ \Omega} \\ \frac{1}{R} &= 2\frac{1}{ \ \Omega} \\ R &= 0.5 \ \Omega \end{align*}Strømmen i hovedkretsen blir da:
\begin{align*} I &= \frac{U}{R} \\ I &= \frac{9 \mbox{ V}}{0.5 \ \Omega} \\ I &= 18 \mbox{ A} \end{align*}Siden parallellkoblingen består av tre like grener, vil strømmen fordele seg likt mellom grenene. Strømmen gjennom hver lampe blir da
\begin{align*} I_l = 18/3 \mbox{ A} = 6 \mbox{ A} \end{align*}Dersom vi kobler til en ekstra lampe i parallell, blir den totale motstanden nå:
\begin{align*} \frac{1}{R} &= \frac{1}{1.5 \ \Omega} + \frac{1}{1.5 \ \Omega} + \frac{1}{1.5 \ \Omega} + \frac{1}{1.5 \ \Omega} \\ \frac{1}{R} &= \frac{4}{ 1.5 \ \Omega} \\ R &= 0.375 \ \Omega \end{align*}Strømmen i hovedkretsen blir da:
\begin{align*} I &= \frac{U}{R} \\ I &= \frac{9 \mbox{ V}}{0.375 \ \Omega} \\ I &= 24 \mbox{ A} \end{align*}Slik som i sted, vil strømmen fordele seg likt mellom grenene. Vi har nå fire grener og strømmen blir dermed:
\begin{align*} I_l = 24/4 \mbox{ A} = 6 \mbox{ A} \end{align*}Samme som i sted.