Magnetisme
Oppgave
Et elektron blir skutt inn mellom to parallelle metallplater med en fart på 10% av lysfarten. Anta at det er en spenning mellom platene slik at vi får et elektrisk felt på \(E = 2.1 \cdot 10^3 \mbox{ N/C}\) som peker nedover (se figuren under). Samtidig er det et magnetfelt \(B = 7.0 \cdot 10^{-4} \mbox{ T}\) mellom platene som peker inn i arket.
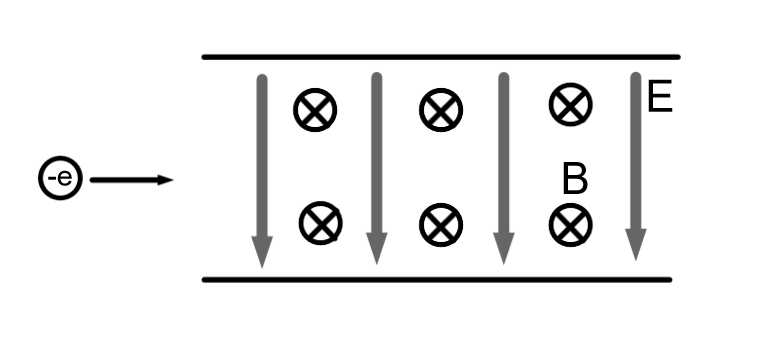
- Tegn på kreftene som virker på elektronet når det beveger seg inni platene og regn ut verdien av disse kreftene (vi ser bort ifra tyngdekraften). Kommer elektronet til å gå rett fremover?
- Anta at avstanden mellom metallplatene er 2.5 cm. Finn arbeidet som den elektriske kraften utfører ved å føre elektronet fra den nederste platen til den øverste.
- Hvor stor er den elektriske spenningen mellom platene?
Løsningsforslag
a)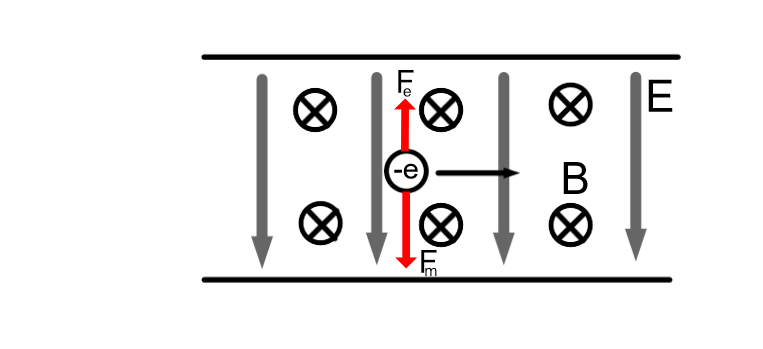
Siden ladninger er negativ, vil kraften på elektronet virke i motsatt retning av det elektriske feltet, dvs. oppover. Vi bruker definisjonen for elektrisk felt og får:
\begin{align*} E &= \frac{F}{q} \\ F &= Eq \\ F &= 2.1\cdot 10^3 \cdot 1.6\cdot 10^{-19} \mbox{ N} \\ F &= 3.36 \cdot 10^{-16} \mbox{ N} \end{align*}Det virker også en magnetisk kraft pga. det magnetiske feltet. Dersom vi bruker høyrehåndsregelen, får vi at en positiv ladning ville blitt dratt oppover av feltet. Siden vi har en negativ partikkel, virker den magnetiske kraften i motsatt retning, dvs. nedover. Vi fikk oppgitt at farten til elektronet var 10% av lysfarten. Dette gir oss:
\begin{align*} F &= qvB \\ F &= 1.6 \cdot 10^{-19} \cdot 0.1\cdot 3\cdot 10^8 \cdot 7\cdot 10^{-4} \mbox{ N} \\ &= 3.36 \cdot 10^{-15} \mbox{ N} \end{align*}Dette er 10 ganger så stor kraft som den elektriske kraften. Dette betyr at elektronet blir dratt nedover av den magnetiske kraften.
b)Elektronet må bevege seg en strekning på \(s=2.5 \cdot 10^{-2} \mbox{ m}\). Dette gir oss et arbeid på:
\begin{align*} W &= Fs \\ &= 3.36 \cdot 10^{-16} \cdot 2.5 \cdot 10^{-2} \mbox{ J} \\ &= 8.4 \cdot 10^{-18} \mbox{ J} \end{align*} c)Spenning er definert som arbeid per ladning. Dette gir oss:
\begin{align*} U &= \frac{W}{q} \\ &= \frac{8.4 \cdot 10^{-18} \mbox{ J}}{1.6 \cdot 10^{-19} \mbox{ C}} \\ &= 52.5 \mbox{ V} \\ &\approx 53 \mbox{ V} \end{align*}