Terningkast og store talls lov

Dette kan ta noen sekunder ved første kjøring dersom bibliotekene ikke allerede installert

Terningkastsimulator

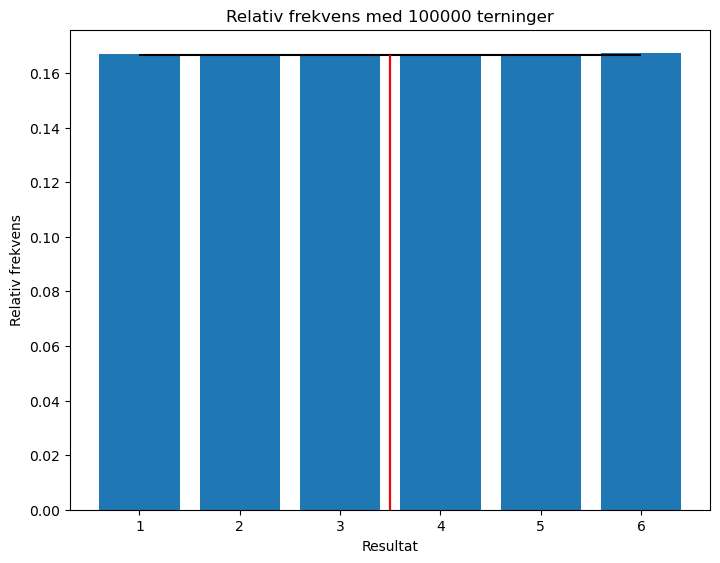
Terningkastsimulator Velg antall sider og antall kast Programmet regner ut gjennomsnitt og relativ frekvens for forsøket, og viser et søylediagram med relativ frekvens.

Programmet illustrerer forskjellen mellom forventningsverdi på det stokastiske forsøket, og det reelle gjennomsnittet i faktiske forsøk.

Ved å øke antall kast kan man vise hvordan store talls lov fungerer

Created on Thu Feb 3 10:27:45 2022

@author: Sigurd Rage, USN

# nødvendige biblioteker
import random
import numpy as np
import matplotlib.pyplot as plt

# setter opp terning og antall kast. Forsøk å øke antall kast og se hva som skjer!
sider = 6
antall_kast = 100000


# Sannsynlighet for hvert utfall beregnet (uniform sannsynlighetsmodell)
sannsynlig_utfall = 1/sider
forventningsverdi = (sider+1)/2

# variabel for å summere terningene i forsøket
minSum = 0
# tabell for å telle antall forekomster av hvert utfall
fordeling = np.zeros(sider)

# kaster terningen, husker sum og antall forekomster
for i in range (0, antall_kast):
    terningkast = random.randint(1, sider)
    minSum += terningkast
    fordeling[terningkast-1]+=1

# regner ut gjennomsnittet og relativ frekvens for hvert utfall
gjennomsnitt = minSum/antall_kast
relativ_frekvens = fordeling/antall_kast
# skriver resultatene til skjerm, sammenligner med beregnede verdier
print("Forventningsverdi til forsøket: " + str(forventningsverdi))
print("Gjennomsnitt i forsøket: " + str(gjennomsnitt))
print("Avvik fra beregnet forventningsverdi: " + str(gjennomsnitt-forventningsverdi))
print()
print("Beregnet sannsynlighet for hvert utfall: " + str(sannsynlig_utfall))
print("Relativ frekvens: " + str(relativ_frekvens))
print("Avvik fra beregnet sannsynlig utfall: " + str(relativ_frekvens-sannsynlig_utfall))

# Lager et søylediagram over relativ frekvens, sannsynlighet for utfall
# angitt med rød linje, gjennomsnitt og forventningsverdi som vertikale linjer
akse = np.linspace(1, sider, sider)
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
ax.bar(akse,relativ_frekvens)
plt.hlines(sannsynlig_utfall, 1, sider, color="black")
plt.vlines(forventningsverdi, 0, sannsynlig_utfall, color="black")
plt.vlines(gjennomsnitt, 0, sannsynlig_utfall, color="red")
plt.title("Relativ frekvens med " + str(antall_kast) + " terninger" )
plt.xlabel("Resultat")
plt.ylabel("Relativ frekvens")
plt.show()

Forventningsverdi til forsøket: 3.5
Gjennomsnitt i forsøket: 3.50016
Avvik fra beregnet forventningsverdi: 0.00016000000000016001

Beregnet sannsynlighet for hvert utfall: 0.16666666666666666
Relativ frekvens: [0.16698 0.16667 0.16666 0.16605 0.16618 0.16746]
Avvik fra beregnet sannsynlig utfall: [ 3.13333333e-04  3.33333333e-06 -6.66666667e-06 -6.16666667e-04
 -4.86666667e-04  7.93333333e-04]