Riemann-summen og det bestemte integral

---

Arealproblemet

Integrasjonsregning er nært knyttet til arealberegning. Fra geometrien har vi mange former vi vet hvordan regne ut arealet til, f.eks. rektangler, trekanter eller sirkler. Noen ganger kan vi derimot få arealer av former formet av funksjoner, f.eks. arealet mellom en funksjon, $f(x)$, og $x$-aksen over et intervall $x \in [a,b]$:

I figuren over ser vi på arealet fra $x=1$ til $x=2$. En fremgangsmåte for å finne en tilnærmet riktig verdi for arealet, er å fylle det med geometriske former vi vet hvordan finne arealet til, f.eks. rektangler.

Arealet av et rektangel er gitt ved høyde multiplisert med bredden av rektangelet. Siden rektangelene nesten passer inn i område mellom funksjonen og $x$-aksen, vil summen av arealene av alle rektanglene gi oss en tilnærmet verdi for det faktiske arealet under funksjonen.

Riemannsummen

Anta at vi har en funksjon $f(x)\geq 0$ på intervallet $x \in[a,b]$. For å fylle arealet med rektangler, deler vi først intervallet opp i $n$ like store delintervaller, $[x_{i-1}, x_i]$ $i=1,2,3,\cdots,n$, med lik bredde $\Delta x = \frac{b-a}{n}$. I hvert delintervall, $[x_{i-1}, x_i]$, velger vi så en tilfeldig $x$-verdi, $x_i^*$, og lager et rektangel med bredde $\Delta x$ og høyde $f(x_i^*)$ (se figuren under).

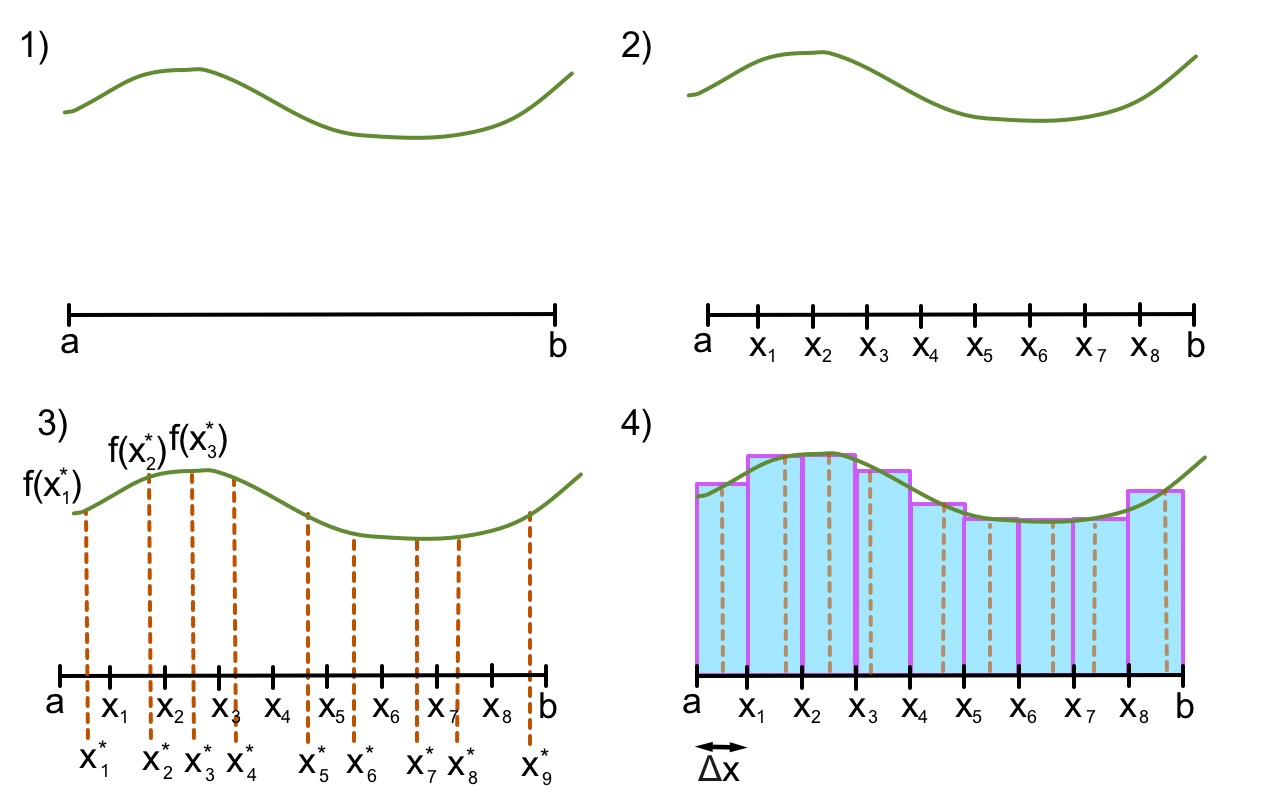
Arealet av rektangel nr. $i$ vil da være gitt med $f(x_i^*)\Delta x$. Dersom vi har mange nok rektangler vil det totale arelaet under funksjonen, $A$, være tilnærmet lik summen av arealene av rektanglene:

\begin{align} A \approx \sum_{i=1}^n f(x_i^*)\Delta x \end{align}

Denne summen kaller vi for en Riemann-sum. Desto flere rektangler vi bruker, desto nærmere ligger summen av rektanglene til det faktiske arealet. Prøv selv å øke antall rektangle i figuren under.

Det faktiske arealet under funksjonen, $A$, blir da grenseverdien til arealet av rektanglene når antall rektangler går mot uendelig:

\begin{align} A = \lim_{n\to \infty} \sum_{i=1}^n f(x_i^*)\Delta x \end{align}

Uttrykket over kaller vi for et bestemt integral. Når $n\to \infty$ vil bredden på rektanglene bli uendelig liten og $\Delta x$ blir et infinitesimal, $\Delta x \to dx$. Vi summerer uendelig mange uendelig små rektangle. I slike tilfeller erstatter man summetegnet $\sum$ med det kjente integrasjonstegnet $\int$. Vi kan tenke på integrasjonstegnet som en slags "kontinuerlig summasjon". Vi går kontinuerlig langs $x$-aksen fra $a$ til $b$ og legger sammen "arealet" av uendelig tynne rektangle. For å illustrere at vi kun ser på funksjonen på intervallet $x\in [a,b]$, legger vi disse på integrasjonstegnet $\int_a^b$. Siden vi går langs alle $x$-verdier, kan vi like godt erstatte $x_i^*$ med $x$ og Riemann-summen får dermed notasjonen:

\begin{align} \lim_{n\to \infty} \sum_{i=1}^n f(x_i^*)\Delta x = \int_a^b f(x) \ dx \end{align}

Forskjellen i notatsjon fra ubestemte integraler, ligger i verdiene på integrasjonsgrensene, $a$ og $b$. Dette viser at vi skal integrere funksjonen fra $x=a$ til $x=b$. Dersom funksjonen er positiv, vil dette gi oss arealet mellom funksjonen vi integrerer og $x$-aksen i dette intervallet. Å se på integrasjon som en "kontinuerlig summasjon" er veldig nyttig i mange sammenhenger blant annet i fysikk og statistikk. Hvordan regne ut et bestemt integral i praksis, vil vi gå gjennom i neste seksjon.