Eksempel 2

Løs integralet $\displaystyle \int \dfrac{1}{x} dx$.

---

Den antideriverte til $1/x$

Å integrere funksjonen $1/x$ kan virke som en triviell oppgave. Dersom vi har en funksjon $F(x) = \ln x$, har vi at $F'(x)=1/x$. Integrerer vi $1/x$, må vi da få funksjonen $\ln x$. Dette er bare en halvvegs sannhet, som vi kan se av figuren under:

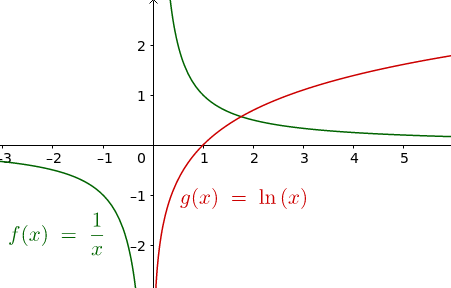
For positive verdier av $x$ vil $\ln x$ være en antiderivert for $1/x$, men vi møter problemer når vi går over til negative $x$-verdier. Her er ikke $\ln x$ definert og kan dermed ikke være en antidertivert for $1/x$.

For å få et inntrykk av hvordan den antivertiverte ser ut for negative $x$-verdier, kan du studere $f(x)=1/x$ som skal angi stigningstallet til sin antiderivert. Eksempelvis har vi:

\begin{align} f(-x) = \frac{1}{-x} = -\frac{1}{x} = -f(x) \end{align}

Stigningstallet til den antideriverte for negative $x$-verdier har stigningstall identisk funksjonen $\ln x$ bare med motsatt fortegn. Når $\ln x$ stiger oppover, vil den antideriverte for negative $x$-verdier synke nedover like bratt. En funksjon som passer denne beskrivelsen er $\ln|x|$:

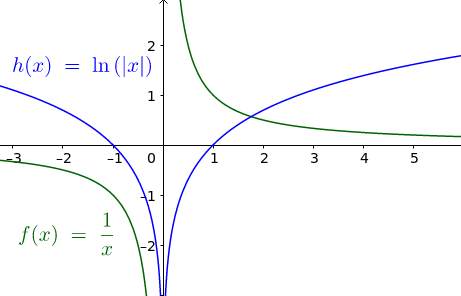
Funksjonen $\ln|x|$ er også identisk $\ln x$ for positive verdier siden der vil $|x|=x$. Vi har dermed at $\ln|x|$ er en mer generell antiderivert for $1/x$ som også gjelder for negative $x$-verdier. Med andre ord:

\begin{align} \int \frac{1}{x} dx = \ln|x| + C \end{align}

Derivere $\ln |x|$

Vi kan sjekke at svaret stemmer ved å derivere $\ln |x|$. Vi bruker regelen for derivasjon av absoluttverdien av en funksjon, $v = v(x)$:

\begin{align} \frac{d|v|}{dx} = \frac{v}{|v|}\cdot \frac{dv}{dx} \end{align}

samt kjerneregelen og får:

\begin{align} \frac{d}{dx}\ln|x| = \frac{1}{|x|}\cdot \frac{d}{dx}|x| = \frac{1}{|x|} \cdot \frac{x}{|x|} \cdot 1 = \frac{x}{|x|^2} = \frac{x}{x^2} = \frac{1}{x} \end{align}

Vi har her bruk at $|x|^2 = x^2$.